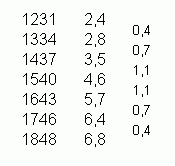Nautisches Lexikon
Exkurs: Zwölftel-Regel
 llen
Ungenauigkeiten zum Trotz: Die Zwölftelregel ist nach wie vor das am häufigsten
angewendete Verfahren der Gezeitenrechnung, genauer: Ein Näherungsverfahren, aber
oft ein gutes. Ihre Beliebtheit verdankt sie der einfachen Merkregel 1-2-3-3-2-1 und der
rechnerischen Einfachheit. Die Zwölftelregel beruht auf der Tatsache, daß eine Gezeitenkurve im
Idealfall einer Cosinuskurve entspricht und sich eine
Cosinuskurve (zufällig) ziemlich gut mit sechs "Zwölftelschritten" annähern läßt,
zwischen denen linear interpoliert wird.
llen
Ungenauigkeiten zum Trotz: Die Zwölftelregel ist nach wie vor das am häufigsten
angewendete Verfahren der Gezeitenrechnung, genauer: Ein Näherungsverfahren, aber
oft ein gutes. Ihre Beliebtheit verdankt sie der einfachen Merkregel 1-2-3-3-2-1 und der
rechnerischen Einfachheit. Die Zwölftelregel beruht auf der Tatsache, daß eine Gezeitenkurve im
Idealfall einer Cosinuskurve entspricht und sich eine
Cosinuskurve (zufällig) ziemlich gut mit sechs "Zwölftelschritten" annähern läßt,
zwischen denen linear interpoliert wird.
Nominelle Genauigkeit
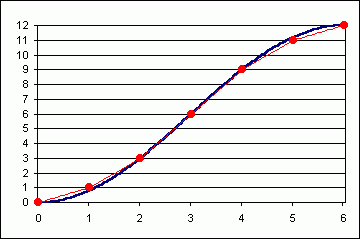
 ie nominelle Genauigkeit der Zwölftelregel ist ziemlich gut. Bei
dem obigen Diagramm sieht man nur bei 1 und 5 eine kleine
Abweichung des roten (Zwölftel-)Punktes von der blauen (Cosinus-)Linie. Die
dünne rote Linie stellt die lineare Interpolation zwischen den roten Punkten
dar, denn zwischen den roten Punkten nimmt man die Gezeit als gleichmäßig steigend (oder fallend)
an. Das entspricht nicht ganz der Realität, aber die Cosinuskurve ist nicht so
krumm, daß sie sich nicht durch mehrere Geradenstücke gut annähern ließe. Das
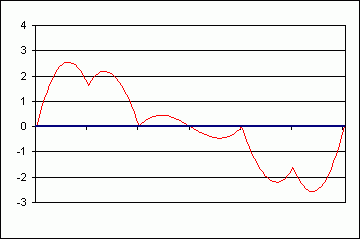
folgende Diagramm zeigt die Abweichung (Fehlerhaftigkeit) der Zwölftelregel von der Cosinuskurve in
Prozent des gesamten Tidenhubs. Man sieht, daß diese Abweichung nie mehr
als 2,5 % beträgt. Bei einem Tidenhub von 3,60 m sind das 10 cm, das ist völlig
ausreichend. Das Problem der Zwölftelregel ist auch weniger ihre nominelle
Ungenauigkeit, sondern eher, dass man ihren Gültigkeitsbereich verlässt (siehe
unten).
ie nominelle Genauigkeit der Zwölftelregel ist ziemlich gut. Bei
dem obigen Diagramm sieht man nur bei 1 und 5 eine kleine
Abweichung des roten (Zwölftel-)Punktes von der blauen (Cosinus-)Linie. Die
dünne rote Linie stellt die lineare Interpolation zwischen den roten Punkten
dar, denn zwischen den roten Punkten nimmt man die Gezeit als gleichmäßig steigend (oder fallend)
an. Das entspricht nicht ganz der Realität, aber die Cosinuskurve ist nicht so
krumm, daß sie sich nicht durch mehrere Geradenstücke gut annähern ließe. Das
folgende Diagramm zeigt die Abweichung (Fehlerhaftigkeit) der Zwölftelregel von der Cosinuskurve in
Prozent des gesamten Tidenhubs. Man sieht, daß diese Abweichung nie mehr
als 2,5 % beträgt. Bei einem Tidenhub von 3,60 m sind das 10 cm, das ist völlig
ausreichend. Das Problem der Zwölftelregel ist auch weniger ihre nominelle
Ungenauigkeit, sondern eher, dass man ihren Gültigkeitsbereich verlässt (siehe
unten).
Praktische Anwendung
 iel
ist die Bestimmung der Lage der "roten Punkte", also die Uhrzeit (x-Achse)
und die Höhe der Gezeit (y-Achse). Bekannt sind diese Werte für den Punkt 0
(Niedrigwasser oben im Bild) und 6 (Hochwasser oben im Bild), Punkt 1 bis 5
wollen wir ermitteln. iel
ist die Bestimmung der Lage der "roten Punkte", also die Uhrzeit (x-Achse)
und die Höhe der Gezeit (y-Achse). Bekannt sind diese Werte für den Punkt 0
(Niedrigwasser oben im Bild) und 6 (Hochwasser oben im Bild), Punkt 1 bis 5
wollen wir ermitteln. |
Zunächst
nimmt man eine Aufteilung von Steig- bzw. Falldauer in sechs
gleiche Intervalle vor:
- Im einfachsten Falle gleich einer Stunde (einfach zu rechnen), oder
- Steigdauer und Falldauer werden mit ihrer realen Dauer angesetzt und durch 6 geteilt (komplizierter, aber
genauer, falls Steigdauer oder Falldauer deutlich von 6 h abweichen). Eine "Rechenstunde" der so
angewendeten Zwölftelregel ist z. B. bei einer Dauer von 6,5 h gleich 65 Minuten
(man muß
nur das Komma der Dauer in h um eine Stelle nach rechts schieben für die
"Rechenstunde" in min).
Anschließend wird der Tidenstieg bzw. -fall durch 12 geteilt,
um das Zwölftel zu erhalten.
Einfaches Beispiel: Tidenstieg von 3,6 m bei einer
Steigdauer von 6 h. Die Anwendung der Regel liefert:
- In der 1. Stunde steigt das Wasser um 1 Zwölftel = 0,3 m.
- In der 2. Stunde steigt das Wasser um weitere 2 Zwölftel = 0,6 m.
- In der 3. Stunde steigt das Wasser um weitere 3 Zwölftel = 0,9 m.
- In der 4. Stunde steigt das Wasser um weitere 3 Zwölftel = 0,9 m.
- In der 5. Stunde steigt das Wasser um weitere 2 Zwölftel = 0,6 m.
- In der 6. Stunde steigt das Wasser um weitere 1 Zwölftel = 0,3 m.
In der Summe sind das die gesamten 3,6 m.
Realistisches, etwas komplexeres Beispiel: Eines, wie man es
den Gezeitentafeln entnehmen könnte (Bezugsort oder Anschlußort). Das rechnet
man dann am einfachsten auf einem Schmierzettel.
NWZ 12:31 h, HWZ 18:47 h
NWH 2,4 m, HWH 6,8 m
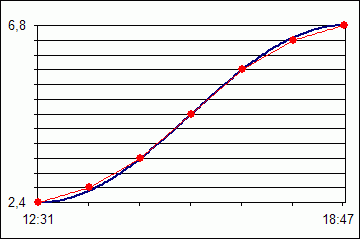
- Berechnung der Basiswerte
Von 12:31 h bis 18:47 h sind es 6 h 16 min. Je 6 min entsprechen einer
Zehntelstunde, das sind also gerundet 6,3 h. Damit ist unsere Rechenstunde
63 min (Komma einfach um eine Stelle nach rechts schieben).
6,8 m -- 2,4 m = 4,4 m. Das muß man durch 12 teilen. Andere Möglichkeit: Durch
10 teilen und vom Ergebnis noch ein Sechstel abziehen: 4,4 m / 10 = 44 cm, ein
Sechstel (etwa 7 cm) davon abziehen, ergibt als Zwölftel 37 cm.
Gerundet ergibt sich 1/12 = 0,4 m, 2/12 = 0,7 m, 3/12 = 1,1 m.
- Aufschreiben der Zeiten
Man fängt mit der ersten Zeit an und addiert einfach immer 63 Minuten dazu,
also 1 h 03 min. Am Ende muß man bei der zweiten Zeit landen (und läßt hier
die paar Minuten Rundungsdifferenz, die sich aus der Berechnung der
Rechenstunde ergeben haben, einfach unter den Tisch fallen):
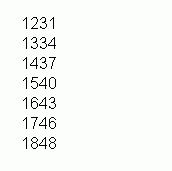
- Aufschreiben der Höhen
Man kann von oben rechnen, von unten oder von beiden Seiten und sich in der
Mitte treffen. Die letzte Spalte ist hier nur der Anschaulichkeit halber
aufgeschrieben, um die Differenzen zu verdeutlichen.
Test: Auf jeden Fall muß die mittlere Höhe genau in der Mitte von HWH und
NWH liegen, sonst hat man einen Fehler gemacht. Hier liegt 4,6 m genau in der
Mitte zwischen 6,8 m und 2,4 m.
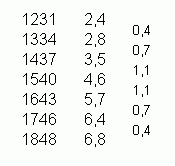
Damit hat man mit wenig Aufwand die wichtigsten Punkte der Gezeitenkurve für
die aktuelle Situation ziemlich genau berechnet. Innerhalb einer Rechenstunde nimmt man an, daß das Wasser linear steigt, also
z. B. linear 0,7 m in den zweiten 63 min. Das ist gut 1 cm pro min. Damit
kann man dann auch Zwischenwerte berechnen, und immer daran denken: Auf 10 cm
mehr oder weniger kommt es nicht an. Das bedeutet nicht, daß man von vornherein
schluren soll, aber man kann die Kirche im Dorf lassen.
- Um 14:00 h beträgt die Höhe der Gezeit etwa 3,1 m (2. Rechenstunde, etwa
1 cm pro min).
- Um 15:30 h beträgt die Höhe der Gezeit etwa 4,4 m (3. Rechenstunde, etwa 2
cm pro min).
- Usw.
Gültigkeitsbereich
 ie
Zwölftelregel geht davon aus, daß der Tidenstieg/Tidenfall einer reinen
Cosinuskurve gehorcht. Wenn diese Voraussetzung halbwegs erfüllt ist (und
häufig ist sie das, vor allem an Orten nahe an tiefem Wasser, z. B. Dover), dann ist das
Verfahren ziemlich genau. Speziell an Orten mit flachem Wasser (Watt) oder
hinter Engstellen (Durchfahrten, Seegatten, Flüsse, ...) sorgt die Reibung am Grund
für Abweichungen von der Cosinus-Form, z. T. recht drastisch. Die Kurve
kann mitunter völlig "verbeult" sein oder mehrere Niedrigwasser oder
Hochwasser kurz hintereinander aufweisen. ie
Zwölftelregel geht davon aus, daß der Tidenstieg/Tidenfall einer reinen
Cosinuskurve gehorcht. Wenn diese Voraussetzung halbwegs erfüllt ist (und
häufig ist sie das, vor allem an Orten nahe an tiefem Wasser, z. B. Dover), dann ist das
Verfahren ziemlich genau. Speziell an Orten mit flachem Wasser (Watt) oder
hinter Engstellen (Durchfahrten, Seegatten, Flüsse, ...) sorgt die Reibung am Grund
für Abweichungen von der Cosinus-Form, z. T. recht drastisch. Die Kurve
kann mitunter völlig "verbeult" sein oder mehrere Niedrigwasser oder
Hochwasser kurz hintereinander aufweisen. |
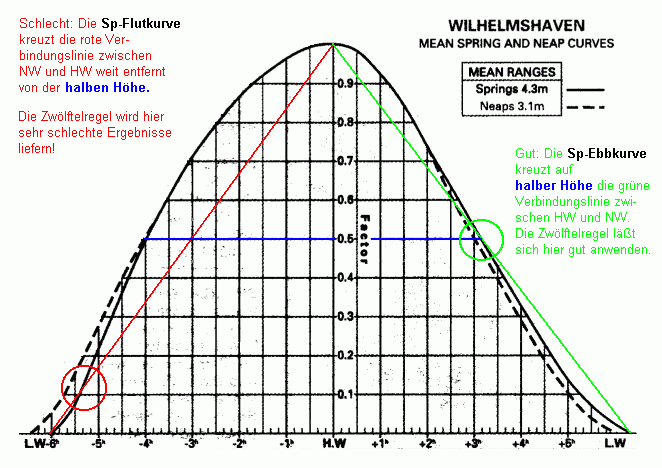
Es gibt erfreulicherweise einen einfachen Test, der einem eine Aussage
darüber gibt, ob eine Cosinuskurve vorliegt, und auch eine Abschätzung über die
Abweichung ermöglicht, falls nicht. Der Test ist getrennt für Flut und Ebbe der
Tidenkurve anzuwenden:
Man verbindet HW und NW auf der Tidenkurve mit einer geraden Linie (rot und grün im
Bild unten). Wenn diese Linie nach der halben Steig- bzw. Falldauer
die Tidenkurve auf der halben Höhe schneidet, hat man allen Grund
anzunehmen, einer ausreichend harmonischen Schwingung gegenüberzustehen, um die
Zwölftel-Regel gut anwenden zu können. Liegt die Tidenkurve nach der halben Steig- bzw.
Falldauer über oder (seltener) unter der halben Höhe, kann man die Abweichung an dieser
Stelle als ungefähres Maß für die maximale Ungenauigkeit der Zwölftelregel ansehen.
Diese Ungenauigkeit kann sehr groß werden, bis hin zur Unbrauchbarkeit!
 llen
Ungenauigkeiten zum Trotz: Die Zwölftelregel ist nach wie vor das am häufigsten
angewendete Verfahren der Gezeitenrechnung, genauer: Ein Näherungsverfahren, aber
oft ein gutes. Ihre Beliebtheit verdankt sie der einfachen Merkregel 1-2-3-3-2-1 und der
rechnerischen Einfachheit. Die Zwölftelregel beruht auf der Tatsache, daß eine Gezeitenkurve im
Idealfall einer Cosinuskurve entspricht und sich eine
Cosinuskurve (zufällig) ziemlich gut mit sechs "Zwölftelschritten" annähern läßt,
zwischen denen linear interpoliert wird.
llen
Ungenauigkeiten zum Trotz: Die Zwölftelregel ist nach wie vor das am häufigsten
angewendete Verfahren der Gezeitenrechnung, genauer: Ein Näherungsverfahren, aber
oft ein gutes. Ihre Beliebtheit verdankt sie der einfachen Merkregel 1-2-3-3-2-1 und der
rechnerischen Einfachheit. Die Zwölftelregel beruht auf der Tatsache, daß eine Gezeitenkurve im
Idealfall einer Cosinuskurve entspricht und sich eine
Cosinuskurve (zufällig) ziemlich gut mit sechs "Zwölftelschritten" annähern läßt,
zwischen denen linear interpoliert wird. 
 ie nominelle Genauigkeit der Zwölftelregel ist ziemlich gut. Bei
dem obigen Diagramm sieht man nur bei 1 und 5 eine kleine
Abweichung des roten (Zwölftel-)Punktes von der blauen (Cosinus-)Linie. Die
dünne rote Linie stellt die lineare Interpolation zwischen den roten Punkten
dar, denn zwischen den roten Punkten nimmt man die Gezeit als gleichmäßig steigend (oder fallend)
an. Das entspricht nicht ganz der Realität, aber die Cosinuskurve ist nicht so
krumm, daß sie sich nicht durch mehrere Geradenstücke gut annähern ließe. Das
folgende Diagramm zeigt die Abweichung (Fehlerhaftigkeit) der Zwölftelregel von der Cosinuskurve in
Prozent des gesamten Tidenhubs. Man sieht, daß diese Abweichung nie mehr
als 2,5 % beträgt. Bei einem Tidenhub von 3,60 m sind das 10 cm, das ist völlig
ausreichend. Das Problem der Zwölftelregel ist auch weniger ihre nominelle
Ungenauigkeit, sondern eher, dass man ihren Gültigkeitsbereich verlässt (siehe
unten).
ie nominelle Genauigkeit der Zwölftelregel ist ziemlich gut. Bei
dem obigen Diagramm sieht man nur bei 1 und 5 eine kleine
Abweichung des roten (Zwölftel-)Punktes von der blauen (Cosinus-)Linie. Die
dünne rote Linie stellt die lineare Interpolation zwischen den roten Punkten
dar, denn zwischen den roten Punkten nimmt man die Gezeit als gleichmäßig steigend (oder fallend)
an. Das entspricht nicht ganz der Realität, aber die Cosinuskurve ist nicht so
krumm, daß sie sich nicht durch mehrere Geradenstücke gut annähern ließe. Das
folgende Diagramm zeigt die Abweichung (Fehlerhaftigkeit) der Zwölftelregel von der Cosinuskurve in
Prozent des gesamten Tidenhubs. Man sieht, daß diese Abweichung nie mehr
als 2,5 % beträgt. Bei einem Tidenhub von 3,60 m sind das 10 cm, das ist völlig
ausreichend. Das Problem der Zwölftelregel ist auch weniger ihre nominelle
Ungenauigkeit, sondern eher, dass man ihren Gültigkeitsbereich verlässt (siehe
unten).
 iel
ist die Bestimmung der Lage der "roten Punkte", also die Uhrzeit (x-Achse)
und die Höhe der Gezeit (y-Achse). Bekannt sind diese Werte für den Punkt 0
(Niedrigwasser oben im Bild) und 6 (Hochwasser oben im Bild), Punkt 1 bis 5
wollen wir ermitteln.
iel
ist die Bestimmung der Lage der "roten Punkte", also die Uhrzeit (x-Achse)
und die Höhe der Gezeit (y-Achse). Bekannt sind diese Werte für den Punkt 0
(Niedrigwasser oben im Bild) und 6 (Hochwasser oben im Bild), Punkt 1 bis 5
wollen wir ermitteln.