Nautisches Lexikon

Exkurs: Erdoberfläche und Referenzflächen

ie Erde ist ein kugelförmiger Planet, der um die Sonne kreist. So weit, so gut. Aber bereits die Frage nach der Höhe eines Berges wirft die Frage auf, was als ideale Form der Erde anzusehen ist. Was bliebe übrig, wenn man alle Berge einebnen würde? Eine perfekte Kugel? Ein Ellipsoid? Oder was Unregelmäßiges? Und wie weit müßte man eigentlich die Berge abtragen? Die Frage nach der idealen Form der Erde, auf deren Oberfläche sich alle Höhenangaben, Tiefenangaben und auch Koordinaten beziehen, ist also in erster Linie eine Frage nach derjenigen Erdoberfläche, die mit "Höhe 0,00 m" anzusetzen ist.
Für den "navigatorischen Hausgebrauch" ist die ideale Form der Erde eine perfekte Kugel. Hieraus leitete sich das geografische Koordinatensystem der Erde mit Längen und Breiten ab, und mit diesem Bild hat man einige Jahrhunderte gut gelebt. Wenn man jedoch genauer hinschaut, dann ist die ideale Form der Erde eher ein Ellipsoid als eine Kugel, weil sich wegen der Fliehkräfte aufgrund der Erdrotation am Äquator ein Wulst gebildet hat, und wenn man noch genauer schaut, dann hat dieses Ellipsoid Beulen und Dellen (die nicht mit den Bergen und Tälern zu verwechseln sind, die sind ja schon abgetragen in unserem Gedankenspiel), was zum Geoid führt. Hier sollen die Ideen der Referenzellipsoide und des Geoids näher erläutert werden, und welche Konsequenzen das für den Umgang mit GPS hat.

Referenzellipsoide

achdem man entdeckt hatte, daß für viele geodätische Probleme die Gestalt der Erde durch eine Kugel nur unzureichend wiedergegeben wird, haben sich die Geodäten besser passende Hilfskörper ausgedacht, die der Form der Erde näher kommen, aber weiterhin gut mathematisch faßbar sind (“Rechenflächen”): Die sogenannten Referenzellipsoide. Das Problem der Kartografen ist nämlich, daß sie nur mit einer mathematisch definierten Figur in der Lage sind, Karten zu zeichnen.

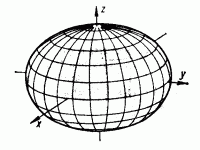Ein Ellipsoid ist durch seine große und kleine Halbachse definiert. Ein Referenzellipsoid für die Erde muß seine Rotationsachse parallel zur Erdrotationsachse haben und seinen Mittelpunkt im Erdmittelpunkt. Diese Festlegung erreicht man dadurch, daß für einen bestimmten Festpunkt in der Natur seine Koordinaten (Länge, Breite, Höhe) definiert werden. Diese Kombination von Ellipsoidabmessung und Referenzpunkt nennt man geodätisches Datum. In jeder Seekarte wird mit dem Kartendatum auf ein bestimmtes Referenzellipsoid Bezug genommen. Leider haben die nationalen Vermessungsämter historisch bedingt fast alle ihr eigenes Datum erfunden, nämlich eines, das für das eigene Land am besten paßte (Potsdamer Datum, Europäisches Datum, Tokyo-Datum etc., sogenannte lokal beste Anpassung). Kriterien für eine solche lokal beste Anpassung waren die geodätische Extrapolation des Meeresspiegels von den Küsten des Landes ins Landesinnere sowie geophysikalische Schwerkraftmessungen, aber halt immer auf den eigenen Landesbereich beschränkt. Es gab keinen globalen Ansatz, der auch rein meßtechnisch für die damalige Zeit zu kompliziert gewesen wäre. Gerechterweise muß man sagen, daß bereits die Referenzellipsoide eine ziemlich revolutionäre Entwicklung waren. Letztendlich "Schuld" an der Entwicklung der verschiedenen Ellipsoide ist die uneinheitliche Form der Erde (Geoid), die sich eben nicht in das schöne Ellipsoid-Schema einordnen läßt.

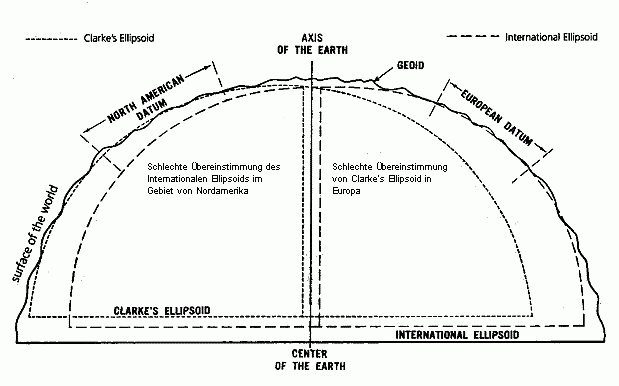
Die folgende Zeichnung veranschaulicht sehr schön schematisch den Unterschied zwischen dem in den USA verwendeten Clarke-Ellipsoid und dem dem Europäischen Datum zugrunde liegenden Internationalen Ellipsoid:

Das Geoid, auch Erdkartoffel genannt

chwerkraftmessungen sind die Basis vieler geowissenschaftlicher Methoden, weil sich z. B. ein Flüssigkeitsniveau immer senkrecht zur Schwerkraftrichtung einstellt (Wasserwaage!). Die ungleichmäßige Massendichte der Erdkruste erzeugt jedoch eine ungleichmäßige Schwerkraftverteilung (z. B. Gebirge: meist tief in die Erdkruste reichende Gebirgs"wurzeln" mit höherer Dichte). Statt eines idealen Ellipsoids hat man also anschaulich eher ein unregelmäßig aus- und eingebeultes Ellipsoid, weshalb die Geodäten auch liebevoll-abfällig von der "Erdkartoffel" sprechen. Nachdem sie mit immer feineren Messungen dahinter gekommen waren, daß auch das Ellipsoid nicht der Weisheit letzter Schluß ist, einigten sich die Geodäten daher auf eine Fläche namens Geoid als ideale Erdoberfläche: Eine gedachte Fläche, die mit dem von Wind- und Gezeiteneinflüssen befreiten mittleren Meeresspiegel zusammenfällt und sich unter den Kontinenten fortsetzt (als wenn diese porös wären). Die Geoid-Fläche schneidet überall die Schwerkraftrichtung senkrecht (Äquipotentialfläche des Schwerkraftfeldes der Erde). Und sie ist nicht nur eine Kopfgeburt der Geodäten, sondern z. B. auch eine wichtige Bezugsfläche für die Flugzeugnavigation.

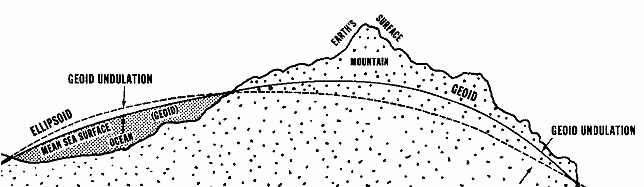Das Nebeneinander der verschiedenen Flächen (Ellipsoid, Geoid und reale Erdoberfläche mit Bergen und Tälern) wird in der rechten Zeichnung recht schön veranschaulicht. Aus der Zeichnung sollte man aber nicht ableiten, daß über dem Meer generell die Schwerkraft größer und in bergigen Gegenden geringer ist. Die Sache ist komplizierter.

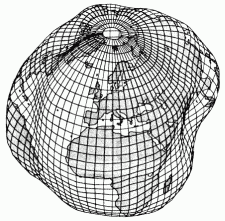Die linke Zeichnung stellt das Geoid für die gesamte Erde stark überhöht (15.000fach) als Ergebnis von Schweremessungen dar. Die größte Mulde (Schwerkraft am größten) befindet sich rechts in der Gegend des Indischen Ozeans (ca. 120 m tiefer als die mittlere Geoidfläche), im Nordatlantik befindet sich ein 65 m hoher Buckel.

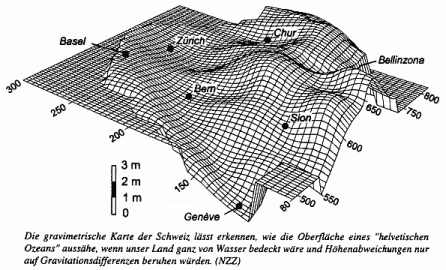Die rechte Zeichnung zeigt, wie sich unter den tatsächlichen Schwerkraftverhältnissen der Schweiz die Meeresoberfläche verhalten würde, und zwar eigentlich nicht das Land bedeckend, sondern unter den (scheinbar porösen) Bergen verlaufend.

Fazit und Folgerungen für GPS

ach dem oben Gesagten können sich die Koordinaten für ein- und denselben Ort je nach geodätischem Datum unterscheiden, und zwar bis zu über eine Seemeile! Meist beträgt der Unterschied jedoch nur wenige Dutzend Meter. Problematisch wird das sowieso erst, wenn man eine Position, die auf einem bestimmten Datum basiert, in eine Seekarte überträgt, die auf einem anderen Datum basiert, und manch ein Schiffsverlust ist solchen Irritationen zuzuschreiben. Aus diesem Grund soll man Positionen aus einer Karte ausschließlich nach Peilung und Abstand zu einem bekannten Objekt, nie nach Länge und Breite in eine andere Karte übertragen.

Weltübergreifende, elektronische Navigationssysteme wie GPS geben einem jedoch Länge und Breite, bei GPS bezogen auf das Datum WGS 84. Daher gibt es mit GPS wieder die alten Probleme, wenn die Seekarte auf dem Kartentisch ein anderes Kartendatum als WGS 84 hat. Erst in jüngerer Zeit werden die internationalen Seekarten nach und nach einheitlich auf WGS 84 umgestellt. So lange wird man mit den Differenzen leben müssen. Die Differenzen zwischen dem Kartendatum und dem WGS 84 sind heutzutage in jeder Karte angegeben.

Um es noch mal zu betonen: Die Differenzen zwischen den unterschiedlichen geodätischen Daten beruhen nicht darauf, daß die Erde mal als Kugel, mal als Ellipsoid und mal als Geoid betrachtet wird, sondern darauf, daß die Form eines theoretischen Ellipsoids und seine Lage zur echten Erde unterschiedlich festgelegt wurden. Es gibt kein "bestes Ellipsoid", sondern mittlerweile nur mehr oder weniger gelungene "internationale Kompromisse", von denen der wichtigste das "GPS-Datum" World Geodetic System von 1984 (WGS 84) ist. Letztendlich ist ja auch die Idee des Geoid mit einem gewissen Maß an Willkür behaftet.